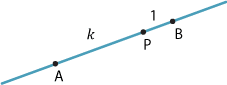Content

Midpoints and division of an interval

Given two points \(A\), \(B\) in the plane, it is clearly possible to create a number line on \(AB\) so as to label each point on \(AB\) with a (real) number.

Line AB with the equal length interval with endpoints labelled from –2 to 2 .
Detailed description

There are (infinitely) many ways in which this can be done, but it turns out not to be particularly useful for geometrical purposes.

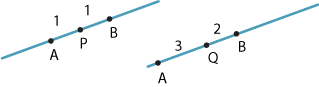
On the other hand, in the following diagrams, we can say that the point \(P\) divides the interval \(AB\) in the ratio \(1:1\) and the point \(Q\) divides the interval \(AB\) in the ratio \(3:2\).

Two lines.
Detailed description

Midpoint of an interval

The midpoint of an interval \(AB\) is the point that divides \(AB\) in the ratio \(1:1\).

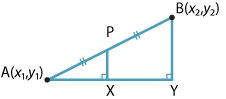
Right-angled triangle AYB.
Detailed description

Assume that the point \(A\) has coordinates \((x_1,y_1)\) and the point \(B\) has coordinates \((x_2,y_2)\). It is easy to see, using either congruence or similarity, that the midpoint \(P\) of \(AB\) is

\[ \Bigl(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\Bigr). \]

This is shown in the module Introduction to coordinate geometry (Years 9–10).

Internal division of an interval

We now generalise the idea of a midpoint to that of a point that divides the interval \(AB\) in the ratio \(k:1\).

Definition

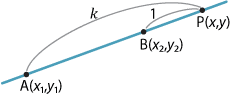
Suppose \(k>0\) is a real number and let \(P\) be a point on a line interval \(AB\). Then \(P\) divides \(AB\) in the ratio \(k:1\) if

\[ \dfrac{AP}{PB} = \dfrac{k}{1}=k. \]

Line AB with point P marked between points A and B with AP = k and PB = 1.
Detailed description

Note. As \(k\to 0\), \(P\to A\) and as \(k\to \infty\), \(P\to B\).

Theorem

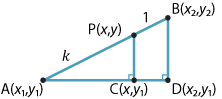
Let \(A(x_1,y_1)\) and \(B(x_2,y_2)\) be two points in the plane and let \(P(x,y)\) be the point that divides the interval \(AB\) in the ratio \(k:1\), where \(k>0\). Then

\[ x = \dfrac{x_1+kx_2}{1+k} \qquad \text{and} \qquad y = \dfrac{y_1+ky_2}{1+k}. \]

Proof

If \(x_1 = x_2\), then it is clear that \(x\) is given by the formula above. So we can assume that \(x_1 \ne x_2\). Consider the points \(C(x, y_1)\) and \(D(x_2, y_1)\), as shown in the following diagram.

Right-angled triangle ABD. Right angle at D.
Detailed description

The triangles \(ACP\) and \(ADB\) are similar (AAA). So \begin{align*} \dfrac{AP}{AB} &= \dfrac{AC}{AD}\\ \dfrac{k}{k+1} &= \dfrac{x-x_1}{x_2-x_1}\\ kx_2-kx_1 &= kx-kx_1+x-x_1\\ (k+1)x &= kx_2+x_1\\ x &= \dfrac{x_1+kx_2}{1+k}. \end{align*}
Similarly, \[ y = \dfrac{y_1+ky_2}{1+k}. \]

\(\Box\)

Exercise 1

If \(P(x,y)\) lies on the interval \(A(x_1,y_1)\), \(B(x_2,y_2)\) such that \(AP:PB = a:b\), with \(a\) and \(b\) positive, show that

\[ x = \dfrac{bx_1+ax_2}{a+b} \qquad \text{and} \qquad y = \dfrac{by_1+ay_2}{a+b}. \]

Screencast of exercise 1

The formulas of Exercise 1 are worth learning.

Example

Let \(A\) be \((-3,5)\) and \(B\) be \((5,-10)\). Find

the distance \(AB\)
the midpoint \(P\) of \(AB\)
the point \(Q\) which divides \(AB\) in the ratio \(2:5\).

Solution

\(AB^2 = \bigl(5-(-3)\bigr)^2+\bigl(-10-5\bigr)^2 = 8^2+15^2 = 17^2\), so \(AB=17\).
\(P\) has coordinates \(\bigl(1,-\dfrac{5}{2}\bigr)\).
\(Q\) has coordinates \[ \Bigl(\dfrac{5\times-3 + 2\times5}{5+2}, \dfrac{5\times5 + 2\times-10}{5+2}\Bigr) = \Bigl(-\dfrac{5}{7}, \dfrac{5}{7}\Bigr). \]

Exercise 2

Give an alternative proof of the previous theorem on internal division of an interval. Use the fact that \(AC = AP\cos\theta\) in the diagram from the proof, where \(\theta = \angle PAC\).

Exercise 3

Suppose points \(A\), \(B\) and \(C\) are not collinear and have coordinates \((x_1,y_1)\), \((x_2,y_2)\) and \((x_3,y_3)\). Let \(D\) be the midpoint of \(BC\) and suppose \(G\) divides the median \(AD\) in the ratio \(2:1\). Find the coordinates of \(G\) and deduce that the medians of \(\triangle ABC\) are concurrent.

External division of an interval

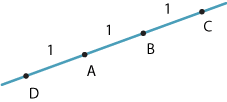
Dividing an interval \(AB\) internally in a given ratio produces a point between \(A\) and \(B\). External division produces a point outside the interval \(AB\).

Line AB drawn with points D and C marked outside of points A and B such that DA = AB = BC = 1.
Detailed description

Suppose \(D\), \(A\), \(B\) and \(C\) are collinear and \(DA=AB=BC\), as in the above diagram. Then

\[ \dfrac{AC}{CB} = \dfrac{2}{1} = 2 \qquad \text{and} \qquad \dfrac{AD}{DB} = \dfrac{1}{2}. \]

We say that \(C\) divides \(AB\) externally in the ratio \(2:1\) and that \(D\) divides \(AB\) externally in the ratio \(1:2\). Clearly this is different from the internal division of an interval discussed in the previous subsection.

In general, suppose that \(P(x,y)\) is on the line \(AB\) but is external to the interval \(AB\) and that \(\dfrac{AP}{PB} = \dfrac{k}{1}\), for some \(k > 0\).

Line AB drawn with point P outside AB. A(x1, y1), B(x2, y2) and P(x, y). AP = k and BP = 1.
Detailed description

Then

\begin{align*} \dfrac{x-x_1}{k} &= \dfrac{x-x_2}{1}\\ x-x_1 &= kx-kx_2\\ x(1-k) &= x_1-kx_2\\ x &= \dfrac{x_1-kx_2}{1-k}. \end{align*}

This suggests that we make the following definition.

Definition

Suppose \(k < 0\) is a real number with \(k \ne -1\) and let \(P\) be a point on a line \(AB\). Then \(P\) divides the interval \(AB\) in the ratio \(k:1\) if \(P\) is external to the interval and

\[ \dfrac{AP}{PB} = -k. \]

With this convention we have

\[ x = \dfrac{x_1+kx_2}{1+k} \qquad \text{and} \qquad y = \dfrac{y_1+ky_2}{1+k} \]

for external division, exactly as for the internal division of an interval! These formulas are algebraically the same as for internal division, but here \(k\) is negative.

Example

Find the coordinates of the point \(P\) which divides the interval \(A(-3,-7)\), \(B(-1,-4)\) externally in the ratio \(4:3\).

Solution

Here \(k = -\dfrac{4}{3}\) and

\begin{align*} x &= \dfrac{-3+\bigl(-\dfrac{4}{3}\bigr)(-1)}{1-\dfrac{4}{3}} = \dfrac{-9+4}{3-4}=5,\\ y &= \dfrac{-7+\bigl(-\dfrac{4}{3}\bigr)(-4)}{1-\dfrac{4}{3}} = \dfrac{-21+16}{3-4}=5. \end{align*}

The point \(P\) has coordinates \((5, 5)\).

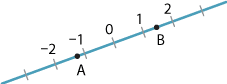
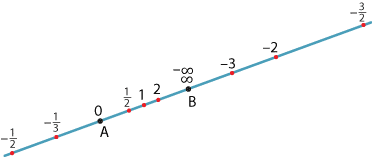
Now, for each point \(P\) on the line \(AB\), we have an associated number \(k\):

for \(P\) in the interval \(AB\), we take \(k=\dfrac{AP}{PB}\)
for \(P\) on the line \(AB\) external to the interval \(AB\), we take \(k=-\dfrac{AP}{PB}\).

The following diagram shows the values of \(k\) for the marked points.

Line AB drawn with points marked, from left to right, minus one half, minus one third, 0 at A, one half , 1, 2, minus infinity and infinity at B, minus 3 and minus 2.
Detailed description

Clearly, as \(P\to\infty\) in either direction, \(\dfrac{AP}{PB}\to -1\). (We are now close to a concept called the real projective line.)

Exercise 4

Suppose \(M\) is the midpoint of \(AB\), where \(A\) is \((8,10)\) and \(B\) is \((18,20)\). Further suppose that \(P\) divides \(AB\) internally and \(Q\) divides \(AB\) externally in the ratio \(2:3\). Show that \(MP \cdot MQ = MB^2\).

Next page - Content - Gradients and the angle of inclination