Volumes of prisms

Volumes of prisms

The volume of a prism is a measure of the space inside the prism.
The units we use to measure volume can be: mm³, cm³ and m³.

To find the volume of a prism, we need to know the area of the base of the solid and the height.

Volume of a Prism	= Area of base × height
V	= Ah

Question 1

Cheesy Moo have created new giant size blocks of cheese to be sold directly to wholesalers. The have found that sales increase dramatically when the cheese is shaped into triangular prisms as shown below.

Find the amount of cheese required for each individual block in cm³.

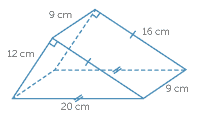
Solution

To find the volume of the triangular prism, first find the area of the base which is a triangle:

Area of the triangular base	= \(\dfrac{1}{2}\)bh
	= \(\dfrac{1}{2}\) × 12 × 16
	= 96 cm²
Volume of a triangular prism	= Ah
	= 96 × 9
	= 864 cm³

Therefore the amount of cheese required to make up one block of cheese is 864 cm³.

Question 2